最新記事
(10/02)
(09/08)
(07/16)
(02/19)
(10/28)
(06/12)
(05/14)
(01/04)
(12/19)
(12/13)
カテゴリー
ブログ内検索

カスタム検索
TradersShop検索
リンク
プロフィール
HN:
さとしぃ
HP:
性別:
男性
趣味:
ゲーム、読書、インターネット
Mail:forexsystecpractice☆gmail.com
☆→@
自己紹介:
06/12/04 立ち上げ。夢のためにFXを06年3月からやっております。
08/05/11 システムトレードの勉強開始。ソフトはMT4を使用。
08/08/06 FXDDにて自動売買を1000ドルの資金で開始。
08/10/09 3000ドルからまさかの大転落。100年に1度の金融危機で生き残ったシステムはたったの三つ。
08/12/09 3000ドルの資金を再投入。 徹底的に本を読み続けています。
09/03/22 7700ドル達成。
09/08/14 1000ドル割れ。
09/12/17 3500ドル復帰。
10/04/09 修行中
14/11/21 パワーアップして再挑戦
06/12/04 立ち上げ。夢のためにFXを06年3月からやっております。
08/05/11 システムトレードの勉強開始。ソフトはMT4を使用。
08/08/06 FXDDにて自動売買を1000ドルの資金で開始。
08/10/09 3000ドルからまさかの大転落。100年に1度の金融危機で生き残ったシステムはたったの三つ。
08/12/09 3000ドルの資金を再投入。 徹底的に本を読み続けています。
09/03/22 7700ドル達成。
09/08/14 1000ドル割れ。
09/12/17 3500ドル復帰。
10/04/09 修行中
14/11/21 パワーアップして再挑戦
アーカイブ
カウンター
RSS
07 November 2025
| [PR]
|
|
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
18 September 2011
| VARでリスク分析
|
検証
|
TB:
|
C:0
|
・VAR
世の中的にはVAR(バリュー・アット・リスク)と呼ばれる指標を用いて、
突発的な損失を予想し、それに対して準備金を備えているそうです。
例えば、
三井住友フィナンシャルグループ
や、
東京三菱UFJ銀行(PDF注意)
などの金融機関にとっても一般的なリスク指標として公開しています。
他の大手銀行も同様です。
今だと、証券も結構そんな感じです。
VARは、統計的アプローチから非常に根拠の示しやすい指標として重宝します。
だからこそ、多くの企業で採用されている実情があります。
・基本的な考え方
基本は、「過去は繰り返す」という態度を取る立場です。
統計的に起こりうる最大損失を過去のデータから予測しようという試みです。
損益というものが個々に独立し、同一の確率分布に従うという前提をとります。
その前提のもと、その損益分布の99%地点の損失額をVARと定義しています。
今回はバックテストデータによりVARを求めてみます。
利用するテストデータは、こちらのテスト結果から使います。
一番信頼しているEAです。
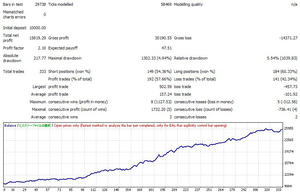
テストデータによる試算および
シミュレーションより求めるモンテカルロ法をテストします。
・テストデータによる試算
2つの考え方があると思います。
①バックテスト時の実現最大損失。
これは簡単でバックテストのconsecutive lossで良いと思います。
②過去損益の確率分布99%点の損失。
こちらは、平均損益 - 2.33 * 損益標準偏差 で求めます。
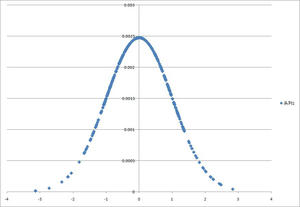
下記グラフは、バックテスト時の損益確率分布図です。

全体損益における1%を占める損失額を見ます。
・モンテカルロ法
バックテスト時の平均損益およびその標準偏差と
1日の平均トレード数およびその標準偏差を用いて、シミュレーションを行い計算します。
前提とする分布は正規分布です。これはバックテスト時の損益の分布から判断します。
今回は、10000回試行し、テストデータにおける実現値との比較を行いました。
結果は以下の画像です。

まず、シミレーションの結果から見ていきます。
当然、VBAマクロで自動化しています。
・平均損益、平気損益標準偏差
これはさすがに近似しますね。
・VAR/1Day
単純に平気損益と平気損益標準偏差より、99%点のVARを求めています。
テスト時の1トレードにおける最大損失に近い値ですね。
1日あたりの損失のため、1トレードあたりより低い値というのは納得出来る範囲だと思います。
これはテストデータにも書いてありますが、1日一回トレードすること自体が稀なためです。
トレードしない日が発生する確率を考慮しているということです。
・一日最大損失
1日おいて発生した最大損失です。
トレード数が極端な回数となり、かつ損が多かった場合に、このような結果が予想されます。
ライブ口座でも、2011/8/7 に、- 473.1pipsを巨額損失を計上しています。
これを見ると、起き得ることだったことが分かります。
ちなみに、1日の最大損失を算出するようにしたのは私がサラリーマンだからです。
1トレードを基準にVARを求めてもあまり意味が薄いと考えています。
自分がシステムに手を加えられるタイムフレームでVARを利用していくべきでしょう。
・最大連日損失
これも面白い結果が出ました。
ライブ口座でも、2011/8/7より2011/8/15の期間で大ドローダウンがこのシステムに訪れるのですが、
実際の最大連日損失は
- 947.6pips
を計上しています。
これはほぼシミレーションの計算と一致する結果となりました。
これもまた、テスト時から想定されることだったのでしょうか。
・まとめ
じっくり取り組んでみましたが、得るものは多かったと思います。
個人的にはVARをオススメします。
上記のテストから改めて、いまのシステムを信ずるに足る根拠が出来たと思います。
また、1日VARを求めて、システムストップ条件に導入するのも良いかもしれません。
実際、8/7の1日最大損失後もDDが続いたため、8/7時点でシステムストップを行うか、
ロットを最小単位にし、監視状態に入るなどの対応も出来たと思います。
・参考書
VARの概要から始まり、確率の基礎、統計の基礎の記述があり、
VARの計算方法が説明されています。
大きな字でとても読みやすく、どう利用していけば良いのかが理解出来ると思います。
統計についても易しいので、統計とVARをまとめて勉強したい方にも入門書としておすすめです。
世の中的にはVAR(バリュー・アット・リスク)と呼ばれる指標を用いて、
突発的な損失を予想し、それに対して準備金を備えているそうです。
例えば、
三井住友フィナンシャルグループ
や、
東京三菱UFJ銀行(PDF注意)
などの金融機関にとっても一般的なリスク指標として公開しています。
他の大手銀行も同様です。
今だと、証券も結構そんな感じです。
VARは、統計的アプローチから非常に根拠の示しやすい指標として重宝します。
だからこそ、多くの企業で採用されている実情があります。
・基本的な考え方
基本は、「過去は繰り返す」という態度を取る立場です。
統計的に起こりうる最大損失を過去のデータから予測しようという試みです。
損益というものが個々に独立し、同一の確率分布に従うという前提をとります。
その前提のもと、その損益分布の99%地点の損失額をVARと定義しています。
今回はバックテストデータによりVARを求めてみます。
利用するテストデータは、こちらのテスト結果から使います。
一番信頼しているEAです。
テストデータによる試算および
シミュレーションより求めるモンテカルロ法をテストします。
・テストデータによる試算
2つの考え方があると思います。
①バックテスト時の実現最大損失。
これは簡単でバックテストのconsecutive lossで良いと思います。
②過去損益の確率分布99%点の損失。
こちらは、平均損益 - 2.33 * 損益標準偏差 で求めます。
下記グラフは、バックテスト時の損益確率分布図です。
全体損益における1%を占める損失額を見ます。
・モンテカルロ法
バックテスト時の平均損益およびその標準偏差と
1日の平均トレード数およびその標準偏差を用いて、シミュレーションを行い計算します。
前提とする分布は正規分布です。これはバックテスト時の損益の分布から判断します。
今回は、10000回試行し、テストデータにおける実現値との比較を行いました。
結果は以下の画像です。
まず、シミレーションの結果から見ていきます。
当然、VBAマクロで自動化しています。
・平均損益、平気損益標準偏差
これはさすがに近似しますね。
・VAR/1Day
単純に平気損益と平気損益標準偏差より、99%点のVARを求めています。
テスト時の1トレードにおける最大損失に近い値ですね。
1日あたりの損失のため、1トレードあたりより低い値というのは納得出来る範囲だと思います。
これはテストデータにも書いてありますが、1日一回トレードすること自体が稀なためです。
トレードしない日が発生する確率を考慮しているということです。
・一日最大損失
1日おいて発生した最大損失です。
トレード数が極端な回数となり、かつ損が多かった場合に、このような結果が予想されます。
ライブ口座でも、2011/8/7 に、- 473.1pipsを巨額損失を計上しています。
これを見ると、起き得ることだったことが分かります。
ちなみに、1日の最大損失を算出するようにしたのは私がサラリーマンだからです。
1トレードを基準にVARを求めてもあまり意味が薄いと考えています。
自分がシステムに手を加えられるタイムフレームでVARを利用していくべきでしょう。
・最大連日損失
これも面白い結果が出ました。
ライブ口座でも、2011/8/7より2011/8/15の期間で大ドローダウンがこのシステムに訪れるのですが、
実際の最大連日損失は
- 947.6pips
を計上しています。
これはほぼシミレーションの計算と一致する結果となりました。
これもまた、テスト時から想定されることだったのでしょうか。
・まとめ
じっくり取り組んでみましたが、得るものは多かったと思います。
個人的にはVARをオススメします。
上記のテストから改めて、いまのシステムを信ずるに足る根拠が出来たと思います。
また、1日VARを求めて、システムストップ条件に導入するのも良いかもしれません。
実際、8/7の1日最大損失後もDDが続いたため、8/7時点でシステムストップを行うか、
ロットを最小単位にし、監視状態に入るなどの対応も出来たと思います。
・参考書
VARの概要から始まり、確率の基礎、統計の基礎の記述があり、
VARの計算方法が説明されています。
大きな字でとても読みやすく、どう利用していけば良いのかが理解出来ると思います。
統計についても易しいので、統計とVARをまとめて勉強したい方にも入門書としておすすめです。
PR

